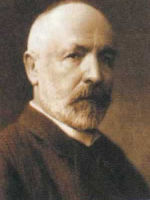 |
Георг Кантор
|
 |
◄►
- -
- Главная
- -
- Сервис
- • Архив
- • Страница
- • Новые поступления
- • Стили оформления
- • Статьи
- • Программы
- • Ссылки
- • OCR Форум
- • Статистика
- • Всей библиотеки
- • Рейтинг@Mail.ru
- • Этой страницы:
-- 6485 пос. (2 сегодня) --
- -
- Библиотека
- • Литература
- • Естествознание
- • Сельское хозяйство
- • Медицина
- • Обществоведение
- • Экономика
- • Филология
- • Философия
- • Искусство
- • • Ноты
- • История
- • Культура, наука, просвещение:
- • • Библиотечное дело
- • • Досуг
- • • Информационная деятельность
- • • Культура
- • • Наука
- • • Памятники, музеи, архивы
- • • Образование, педагогика
- • • СМИ
- • • Физкультура и спорт
- • • Физкультура и спорт: Моделизм
- • • Физкультура и спорт: Шахматы
- • Политика
- • Право
- • Психология и Психиатрия
- • Религия
- • Военное дело
- • Художественная
- • Техника
- • Универсальная
- -
- Поиск
- -
- Справка
- -
- Почта
Универсальная библиотека, портал создателей электронных книг. Только для некоммерческого использования!
